728x90
반응형
PCA 응용분야(그림: ChatGPT4o 생성)
아래에 PCA(주성분 분석)의 주요 응용 분야, 역할, 그리고 사용 이유 및 장점을 상세히 정리해드릴게요.
📌 PCA의 응용 분야 (Applications of PCA)
1. 📊 데이터 시각화
- 목적: 고차원 데이터를 2D 또는 3D로 줄여 그래프로 시각화
- 예시:
- 이미지 데이터 시각화 (예: MNIST 손글씨)
- 텍스트 임베딩의 군집 형태 확인
2. 🧠 머신러닝 전처리
- 목적: 모델 훈련 전 차원을 줄여 과적합 방지 및 속도 향상
- 예시:
- SVM, k-NN 등 거리 기반 알고리즘의 성능 개선
- 다중공선성 제거 (Multicollinearity 해결)
3. 🧬 유전자 데이터 분석 (Bioinformatics)
- 목적: 수천 개 유전자 중 유의미한 패턴 추출
- 예시:
- 질병 유전자 식별
- 샘플 간 유사도 시각화
4. 🎨 이미지 압축
- 목적: 이미지의 정보 손실을 최소화하며 파일 크기 줄이기
- 예시:
- 고해상도 이미지를 주성분만 남겨 저장
- 얼굴 이미지에서 특징만 추출 (Eigenfaces)
5. 🔍 이상 탐지 (Anomaly Detection)
- 목적: 정상 패턴에서 벗어난 이상값 탐지
- 예시:
- 금융 사기 탐지
- 기계 상태 모니터링에서 고장 징후 발견
🧠 PCA의 역할 (What PCA Does)
|
역할
|
설명
|
|
🧭 방향 찾기
|
데이터가 가장 많이 퍼진 방향(정보가 많은 축)을 찾음
|
|
📉 차원 축소
|
주요 정보만 남기고 나머지를 제거함
|
|
🧼 잡음 제거
|
불필요한 잡음을 줄이고 중요한 패턴만 남김
|
|
🔍 패턴 강조
|
데이터의 주요 구조를 더 명확하게 보여줌
|
✅ PCA를 사용하는 이유 (Why Use PCA?)
1. 차원 축소로 인한 학습 효율 향상
- 입력 특성 수가 줄어들면 모델이 더 빠르게 학습
- 고차원 공간에서 발생하는 "차원의 저주(Curse of Dimensionality)" 완화
2. 데이터 시각화 가능
- 사람 눈으로 보기 힘든 고차원 데이터를 2차원으로 축소하여 패턴 이해에 도움
3. 중복 제거 및 노이즈 감소
- 상관관계가 높은 변수들을 통합하여 중복 제거
- 작은 고유값 방향 제거 → 노이즈 감소
4. 모델 성능 개선
- 불필요한 변수 제거로 과적합 방지
- 예측 성능이 안정화됨
💡 요약 정리
|
구분
|
내용
|
|
🎯 목적
|
중요한 정보만 남기고 데이터 단순화
|
|
🔍 역할
|
정보 압축, 방향 재설정, 잡음 제거
|
|
🧩 장점
|
시각화, 모델 효율, 노이즈 제거
|
|
🛠 사용 분야
|
이미지 처리, 생물정보학, 이상탐지, 전처리 등
|
🇰🇷 머신러닝 전처리 PCA 활용 코드
from sklearn.datasets import load_iris
import load_iris from sklearn.decomposition
import PCA from sklearn.preprocessing
import StandardScaler from sklearn.model_selection
import train_test_split from sklearn.neighbors
import KNeighborsClassifier from sklearn.metrics
import accuracy_score
# 1. 데이터 불러오기 iris = load_iris() X, y = iris.data, iris.target
# 2. 표준화 scaler = StandardScaler() X_scaled = scaler.fit_transform(X)
# 3. PCA 적용 (차원을 2개로 축소) pca = PCA(n_components=2) X_pca = pca.fit_transform(X_scaled)
# 4. 학습/테스트 분할 X_train, X_test, y_train, y_test = train_test_split(X_pca, y, test_size=0.3, random_state=42)
# 5. 거리 기반 분류기 (k-NN) 학습 knn = KNeighborsClassifier(n_neighbors=3) knn.fit(X_train, y_train)
# 6. 예측 및 정확도 평가 y_pred = knn.predict(X_test) print("정확도:", accuracy_score(y_test, y_pred))
✅ 설명
- StandardScaler로 스케일 차이 제거
- PCA로 차원을 4개 → 2개로 축소
- k-NN 같은 거리 기반 알고리즘의 성능 개선
- 다중공선성 문제도 PCA로 완화됨
📌 PCA에서 차원 축소 개수 결정 방법
1. ✅ 누적 설명 분산 비율 (Cumulative Explained Variance Ratio)
- 각 주성분은 전체 분산 중 얼마나 많은 정보를 설명하는지를 나타냅니다.
- 보통 95% 이상 설명하는 지점까지의 주성분 수를 선택합니다.
🔹 예:
- PC1: 70%
- PC2: 20%
- PC3: 5%
- → 총 3개로 95% 설명하므로, 3개 사용 결정
2. 📉 Scree Plot (스크리 플롯)
- 각 주성분의 설명 분산량을 선 그래프로 표현한 것
- 꺾이는 지점(elbow point)까지 사용하는 것이 일반적입니다.
🧪 예제 코드 (Iris 데이터 기준)
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np
# 1. 데이터 로드 및 표준화
data = load_iris()
X = data.data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 2. PCA 적용 (전체 주성분 추출)
pca = PCA()
pca.fit(X_scaled)
# 3. 설명 분산 비율 출력
explained_var = pca.explained_variance_ratio_
cumulative_var = np.cumsum(explained_var)
print("개별 설명 비율:", explained_var)
print("누적 설명 비율:", cumulative_var)
# 4. 시각화 - Scree Plot
plt.figure(figsize=(8, 5))
plt.plot(range(1, len(cumulative_var)+1), cumulative_var, marker='o', linestyle='--')
plt.axhline(y=0.95, color='r', linestyle='-')
plt.xlabel('Number of Principal Components')
plt.ylabel('Cumulative Explained Variance')
plt.title('Cumulative Explained Variance by PCA Components')
plt.grid(True)
plt.show()
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np
# 1. 데이터 로드 및 표준화
data = load_iris()
X = data.data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 2. PCA 적용 (전체 주성분 추출)
pca = PCA()
pca.fit(X_scaled)
# 3. 설명 분산 비율 출력
explained_var = pca.explained_variance_ratio_
cumulative_var = np.cumsum(explained_var)
print("개별 설명 비율:", explained_var)
print("누적 설명 비율:", cumulative_var)
# 4. 시각화 - Scree Plot
plt.figure(figsize=(8, 5))
plt.plot(range(1, len(cumulative_var)+1), cumulative_var, marker='o', linestyle='--')
plt.axhline(y=0.95, color='r', linestyle='-')
plt.xlabel('Number of Principal Components')
plt.ylabel('Cumulative Explained Variance')
plt.title('Cumulative Explained Variance by PCA Components')
plt.grid(True)
plt.show()
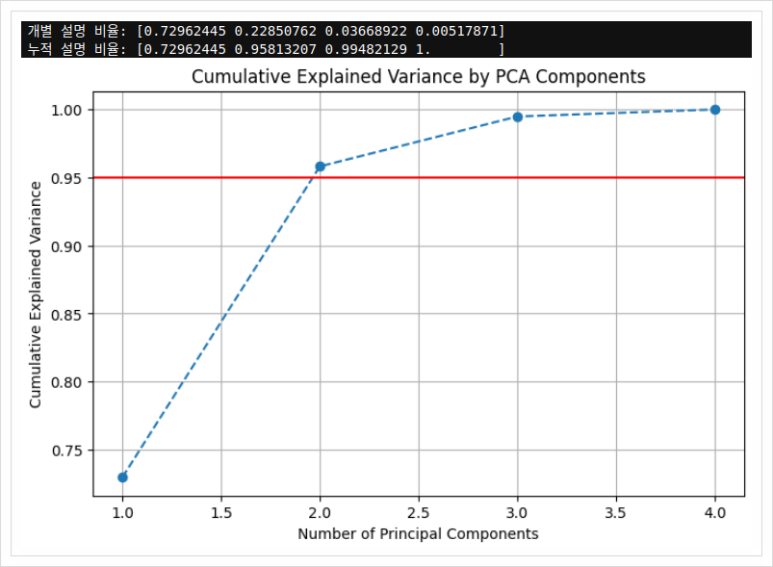
결과
🎯 해석 방법
- 출력되는 누적 설명 분산(cumulative explained variance)을 보고
- 0.95 이상이 되는 최소 주성분 수를 선택합니다.
- 그래프에서 빨간선이 95%선입니다.
- 그 선을 넘는 첫 번째 지점이 우리가 선택할 차원 수입니다.
📌 요약
|
방법
|
설명
|
사용 기준
|
|
누적 설명 분산
|
몇 개의 주성분이 전체 정보를 얼마나 설명하는지
|
일반적으로 95% 이상
|
|
Scree Plot
|
주성분별 설명 비율을 시각화한 꺾은선 그래프
|
Elbow point 찾기
|
반응형
'데이터전처리' 카테고리의 다른 글
| 데이터 전처리 기법: Autoencoder를 활용한 차원 축소 및 특징 추출 (0) | 2025.04.16 |
|---|---|
| 데이터 전처리 기법: Feature Interaction 완전 가이드 (0) | 2025.04.16 |
| 데이터 전처리 기법: 고유값 분해 (0) | 2025.04.14 |
